Prev : Distribusi/Statistik Maxwell-Boltzmann (Energi Rata-rata Partikel dan Energi Dalam)
Pada artikel sebelumnya, kita telah menentukan energi partikel rata-rata dari suatu sistem yang berada dalam keseimbangan termal dengan suhu T, yang kita temukan dapat diungkapkan dengan hubungan
 (1)
(1)
Perlu dicatat bahwa energi yang dimaksud dari Persamaan (1) ini adalah energi total sistem. Artinya, energi tersebut sudah termasuk gerakan-gerakan atau sumber energi lain yang dimiliki oleh partikel-partikel didalamnya, seperti gerak lurus (translasi), berputar (rotasi), bergetar (vibrasi), dan energi potensial gravitasi terhadap Bumi. Menggunakan distribusi Maxwell-Boltzman, kita pada dasarnya dapat menentukan energi total atau energi rata-rata dari masing-masing ketiga sumber gerakan partikel yang telah dijelaskan sebelumnya. Kita akan menggunakan prosedur yang sama, dengan mengingat bahwa kali ini E adalah

dimana m adalah massa partikel yang bergerak secara translasi dengan kecepatan v. sehingga fungsi probabilitas dari distribusi Maxwell-Boltzmann P(v) menjadi
 (2)
(2)
Untuk menentukan Z, hubungan normalisasi harus dipenuhi

Ada beberapa hal yang perlu diperhatikan terkait dengan batas bawah dan atas integral. Pertama, kita menggunakan batas bawah negatif tak hingga, mengingat bahwa partikel dapat bergerak ke arah kanan atau ke arah kiri dalam satu dimensi. Kedua, apabila kita telah mempelajari teori relativitas Einstein, kita tahu bahwa seharusnya batas bawah dan atas adalah –c dan c, dimana c adalah kecepatan cahaya, mengingat bahwa c merupakan batas kecepatan maksimum partikel. Namun, penggunaan nilai tak hingga ini dilakukan agar konsisten dengan batas atas energi total yang telah kita kaji sebelumnya, yaitu tak hingga, dimana apabila energi kinetik partikel tak hingga, maka kecepatan partikel harus tak hingga pula apabila massa partikel memiliki nilai berhingga atau finite. Selain itu, dengan menggunakan batas ini, kita dapat secara langsung mengevaluasi integral, dengan mengingat bahwa

Dengan demikian apabila kita ambil

maka syarat normalisasi menjadi

sehingga

dan Persamaan (2) menjadi
 (3)
(3)
yang merupakan fungsi rapat probabilitas kecepatan partikel.
Dari Persamaan (3) ini kita dapat menentukan energi kinetik rata-rata partikel, dengan hubungan
 (4)
(4)
Apabila kita anggap semua partikel memiliki massa yang sama, maka Persamaan (4) menjadi
 (5)
(5)
Dengan kata lain, untuk menentukan rata-rata energi kinetik, kita perlu menentukan <v²>, atau rata-rata kuadrat dari kecepatan masing-masing partikel. Apabila kecepatan partikel terdistribusi dengan fungsi distribusi pada Persamaan (3), maka secara kontinu nilai rata-rata kuadrat kecepatan adalah
 (6)
(6)
Perlu dicatat bahwa dalam Persamaan (6) ini, kita pada dasarnya mengalikan v² dengan fungsi distribusi P(v), sehingga produk tersebut perlu diintegralkan dengan dv. Memasukkan Persamaan (3) ke (6) akan kita peroleh

Seperti sebelumnya, karena

maka
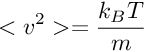 (7)
(7)
Apabila kita masukkan Persamaan (7) ke (5), kita peroleh
 (8)
(8)
Persamaan (8) adalah ungkapan untuk energi kinetik rata-rata dari partikel yang bergerak secara translasi dalam satu dimensi. Untuk partikel tiga dimensi, kita dapat menggunakan fakta bahwa resultan dari kecepatan dapat dinyatakan dengan

sehingga energi kinetik rata-rata dalam tiga dimensi adalah

Apabila tiap dimensi menyumbangkan nilai kBT/2 yang sama, maka kita peroleh
 (9)
(9)
Ungkapan energi kinetik rata-rata pada Persamaan (9) adalah besar energi kinetik yang seharusnya kita peroleh untuk sistem dimana partikel-partikel di dalamnya hanya memiliki energi kinetik translasi saja. Partikel-partikel yang memiliki fitur seperti ini adalah partikel atau gas monoatomik seperti helium (He), neon (Ne), dan lain sebagainya yang memiliki hanya satu unsur atom.