Usaha Total pada Sistem Banyak Muatan

Prev : Beda Potensial dan Curl dari E

Kita telah mempelajari bahwa gaya Coulomb termasuk gaya konservatif, sehingga dapat dinyatakan dalam bentuk energi potensial. Dengan mengetahui energi potensial antar muatan, kita dapat mengetahui usaha total pada suatu sistem dengan bermacam-macam muatan.

Sekarang, katakanlah bahwa kita ingin memindahkan ketiga muatan sehingga ketiga muatan tersebut akan tersusun seperti berikut.

Kita dapat memindahkan ketiga muatan satu per satu. Apabila kita memindahkan partikel pertama (q1), maka tidak ada usaha yang kita lakukan karena tidak ada medan listrik dari muatan lain. Kemudian ketika memindahkan partikel kedua (q2) ke titik tujuan, maka kita perlu melakukan usaha sebesar

Selanjutnya, kita memindahkan partikel ketiga (q3). Karena dalam sistem sudah terdapat q1 dan q2, maka usaha yang diperlukan untuk memindahkan partikel ketiga adalah

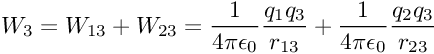
Sehingga usaha total pada sistem adalah

Ini adalah usaha total dari sistem. Perhatikan bahwa kita tidak perlu memperhitungkan W21, W31, dan W32, karena sudah diwakilkan oleh W12, W13, dan W23. Dengan demikian, apabila kita memiliki N partikel, maka

dimana i > j. Kita bisa melakukan suatu trik supaya syarat i > j hilang, mengingat bahwa

sehingga

Ini adalah usaha total yang kita inginkan untuk sistem N partikel, dengan memperhitungkan total potensial yang diderita oleh masing-masing partikel. Perlu dicatat bahwa syarat persamaan diatas bukan lagi i > j, melainkan berkurang menjadi i ≠ j, dan rij = rji, karena kita hanya memperhitungkan skalarnya.

Tentunya kita bisa mengembangkan persamaan ini untuk kasus persebaran muatan kontinu. Untuk kasus muatan kontinu, persamaan di atas bukan lagi kita tuliskan sebagai penjumlahan total, melainkan kita representasikan sebagai bentuk integral, yaitu

Kita dapat menyatakan dq sebagai bentuk diferensial dari rapat muatan ρ dalam ruangan dτ, dimana

sehingga

Kita dapat menggunakan persamaan Maxwell I untuk mensubstitusikan ρ, dimana

sehingga

Kemudian dengan menggunakan analisis vektor, dimana

maka akan kita peroleh

Mengingat bahwa E=-∇φ, maka

Pada ruas pertama kita bisa gunakan teorema Gauss, dan pada ruas kedua, E • E = E², sehingga

Ini adalah usaha total yang kita perlukan untuk menyusun muatan dengan distribusi kontinu, atau kita dapat katakan sebagai energi total sistem. Pada suku pertama, kita mengintegrasikan kuadrat medan listrik terhadap ruangan sistem, dan pada suku kedua, kita mengintegrasikan produk dari medan listrik dan potensial terhadap permukaannya.

Namun, kita dapat melakukan trik lain dari persamaan di atas. Apabila kita perbesar integrasi terhadap volume, tentunya suku kedua otomatis harus mengecil, berdasarkan hukum kekekalan energi, dimana W harus selalu bernilai tetap ketika kita perbesar ruang integrasinya (atau dengan kata lain, kita hanya memperluas pandangan kita, tidak menambah energi sistem). Dengan demikian, apabila kita terus perluas ruang integrasi kita seluas mungkin, tentunya suku kedua harus semakin mengecil, dan kemudian kita peroleh bahwa suku kedua harus bernilai, atau setidaknya mendekati nol dan dapat diabaikan, sehingga kita dapat tulis kembali persamaan di atas menjadi

Disini kita tambahkan persamaan sebelumnya dengan catatan “all space“, menandakan bahwa kita mengintegrasikan semua ruangan yang ada, tidak hanya dalam sistem saja.