Prev : Momen Inersia Pada Benda Banyak
Pada pembahasan sebelumnya kita telah mengetahui cara menghitung momen inersia pada suatu sistem dengan massa yang bervariasi di beberapa titiknya dari sumbu rotasi berada di pusat massa. Namun, apa yang terjadi apabila sumbu rotasinya berubah?

Anggaplah bahwa kita ingin mengubah sumbu rotasi dari Icm menjadi I’. Pada gambar di atas, r1 dan r2 berturut turut adalah jarak antara beban dengan massa m1 dan m2 ke titik pusat massa, sedangkan r1′ dan r2′ adalah jarak kedua beban dari titik sumbu rotasi baru. Pada dasarnya kita dapat menuliskan

Namun, kita juga dapat menuliskannya sebagai

sehingga

atau kita dapat merapihkannya menjadi
 (1)
(1)
Pada suku pertama, kita dapat mendefinisikannya menjadi MR², dimana M adalah massa total sistem (dalam hal ini adalah massa beban 1 ditambah massa beban 2) dan R = r_cm. Sedangkan suku kedua tidak lain adalah momen inersia sistem ketika sumbu rotasi terletak pada pusat massa (Icm).
Namun, untuk suku terakhir agak rumit. Apabila kita asumsikan koordinat pusat (titik nol) terletak pada pusat massa Lr, maka pada umumnya kita menulis

Namun, karena kedua beban terletak pada tempat yang berlawanan (beban 1 berada di kiri dan beban 2 berada di kanan), maka persamaannya akan berubah menjadi
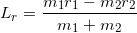
sehingga Persamaan (1) menjadi
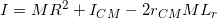
Karena sebelumnya kita telah mendefinisikian bahwa titik nol berada pada pusat massa, maka kita dapat menyimpulkan bahwa Lr = 0, sehingga kita peroleh

Teorema ini disebut sebagai teorema sumbu sejajar, yaitu suatu teorema yang berguna untuk menentukan momen inersia suatu benda pada sumbu rotasi yang baru. Kita dapat menggunakan teorema ini apabila kita telah mengetahui letak pusat massa serta momen inersia pada sumbu rotasi di pusat massa, sehingga untuk mengetahui momen inersia yang baru, kita hanya perlu menimbang beban yang hendak diputar, serta mengukur jarak antara titik pusat massa dengan titik sumbu rotasi yang baru.