Vektor – Perkalian Vektor : Produk Luar (Cross Product)

Prev : Vektor – Dimensi Ketiga

Sebelumnya kita telah memperoleh adanya dimensi ketiga, menggunakan analogi penentuan luas persegi panjang dengan vektor. Kita juga peroleh hubungan vektor sebagai berikut

Dalam vektor, perkalian vektor ini disebut sebagai perkalian cross (cross product), atau produk luar. Produk luar dari dua vektor akan menghasilkan suatu vektor baru, dan ditandai oleh operator “×” (dibaca cross)

sehingga secara lengkap, hubungan antar vektor dapat ditulis sebagai

dengan tambahan bahwa

Ini sesuai dengan analogi bahwa apabila kita mengambil dua vektor yang memiliki arah yang sama, kita akan memperoleh luas antara kedua vektor bernilai nol. Lihat artikel sebelumnya.

Kita bisa menuliskan dua vektor sebagai berikut

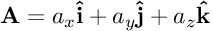
Maka produk luarnya adalah

Ini adalah penyelesaian umum dari perkalian cross antara dua vektor. Apapun vektornya yang tertulis menggunakan notasi vektor koordinat Cartesian akan memiliki penyelesaian umum seperti di atas.

Sebagai contoh, tinjau dua vektor berikut

Menggunakan bentuk penyelesaian yang telah kita peroleh sebelumnya, maka kita hanya perlu memasukkan parameter-parameter vektor ke dalam penyelesaian umum saja untuk menentukan produk luar dari A terhadap B, maka

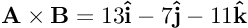
Namun, apabila kita tukar posisinya, sehingga menjadi B × A, maka produk luarnya adalah

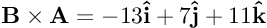
Seperti yang kita lihat, apabila kita tukar perkaliannya, maka nilainya akan menjadi negatif. Dengan demikian, kita peroleh hubungan

Visualisasi vektornya dapat kita lihat pada gambar berikut