Prev : Kalkulus : Turunan – Turunan Trigonometri (Fungsi Tan x)
Sejauh ini kita telah membahas konsep dasar dari turunan, serta mengetahui turunan dari beberapa fungsi seperti fungsi polinomial dan beberapa fungsi-fungsi trigonometri. Namun kita masih belum membahas kegunaan dari konsep turunan ini sebenarnya. Dengan kata lain, kita telah mengetahui filosofi atau konsep dasar dari turunan, dan kita telah mengetahui turunan dari suatu fungsi, namun kita belum mengetahui mengapa kita perlu menurunkan suatu persamaan atau fungsi. Sekarang kita akan mulai membahas aplikasi dari turunan untuk menganalisa atau memecahkan suatu kasus.
Untuk menjawab pertanyaan tentang kegunaan turunan tersebut, kita akan kembali ke konsep paling mendasar dari turunan. Kita akan meninjau suatu fungsi sembarang y = f(x) yang dapat digambarkan oleh gambar berikut ini
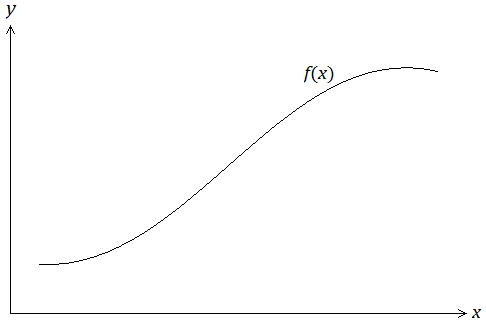
Apabila kita turunkan fungsi f(x) tersebut, maka yang akan kita peroleh adalah kemiringan dari fungsi f(x) untuk setiap nilai x. Dengan kata lain, kemiringan fungsi f(x) ketika x = a akan bernilai sebesar f’(a), dan ketika x = b, nilainya akan sebesar f’(b), dan seterusnya, seperti pada gambar berikut

dimana dua garis lurus yang baru tepat bersinggungan dengan kurva f(x) sehingga kemiringan kedua garis tersebut adalah f’(a) dan f‘(b).
Nilai dari ca dapat ditentukan dengan mensubstitusikan y dengan f(a), mengingat y = f(a) pada x = a. Dengan demikian kita peroleh hubungan
 (1)
(1)
sehingga kita peroleh persamaan garis singgung di titik x = a adalah

 (2)
(2)
Sebagai contoh, kita akan meninjau fungsi kuadrat sederhana, yaitu f(x) = x², sehingga f’(x) = 2x. Maka persamaan garis singgung di titik a dapat dituliskan sebagai
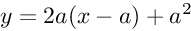

Misal, untuk a = 1, maka


Selanjutnya kita akan membahas kasus dimana gradien garis singgung suatu kurva bernilai nol. Dalam kasus ini kita akan memiliki analisa yang lebih dalam, bergantung dengan konteks kasus yang akan kita kaji.